บทที่1 เซต

บทที่ 1 เรื่องเซต วิชาคณิตศาสตร์พื้นฐาน

เซต เป็นคำที่ไม่ให้ให้นิยาม (Undefined Term) เรามักใช้เซตแทนสิ่งที่อยู่ร่วมกัน ซึ่งหมายถึงกลุ่มของสิ่งต่างๆ ที่เราสามารถกำหนดสมาชิกได้ชัดเจน (Well-Defined) หรือก็คือความหมายของเซตนั่นเอง การเขียนเซต 1. เขียนแบบแจกแจงสมาชิก (Tabular Form) เป็นการเขียนเซตโดยบรรจุสมาชิกทั้งหมดของเซตลงในวงเล็บปีกกา และระหว่างสมาชิกแต่ละตัวคั่นด้วยเครื่องหมายจุลภาค (,) เช่น {A,B,C} หรือ {1, 2, 3} เป็นต้น (หมายเหตุ: ถ้าเซตมีจำนวนสมาชิกมากมาย เราใช้ “…” แทนสมาชิกที่เหลือ) 2. เขียนสับเซตแบบบอกเงื่อนไขของสมาชิกในสับเซต (Set builder form) มีหลักการ คือ แทนสมาชิกของเซตด้วยตัวแปรแล้วกำหนดเงื่อนไขเกี่ยวกับตัวแปรนั้น เพื่อแสดงว่ามีสิ่งใดบ้างที่เป็นสมาชิกของเซต วิธีเขียนเซตโดยวิธีนี้ คือ เขียนตัวแปรและสิ่งที่กำหนดเงื่อนไขเกี่ยวกับตัวแปรลงในวงเล็บปีกกาและคั้นตัวแปรกับสิ่งที่กำหนดเงื่อนไขเกี่ยวกับตัวแปรด้วยเครื่องหมาย “|” หรือ “:”  3. การเขียนเซตด้วยวิธีอื่นๆ เช่น แบบบรรยาย, แบบใช้แผนภาพเวนน์, แบบช่วง เป็นต้น แผนภาพเวนน์-ออยเลอร์ เป็นแผนภาพที่ใช้เขียนแทนเซตซึ่งแทนเอกภพสัมพัทธ์ U ด้วยสี่เหลี่ยมผืนผ้า และแทนเซต A, B, … ด้วยรูปวงกลม หรือวงรี หรือรูปปิดอื่นๆ ดังรูป รูปวงรี แทนเซต A โดยที่ A = {1, 2, 3} รูปวงกลม แทนเซต B โดยที่ B = {a, b, c} รูปสามเหลี่ยม แทนเซต C โดยที่ C = {4,5}  ซึ่งในเรื่องของแผนภาพนี้เรายังทำไปประยุกต์ใช้ในเรื่องการกระทำระหว่างเซต ซึ่งแสดงด้วยแผนภาพจะทำให้ดูเข้าใจง่ายขึ้น เนื้อหาคณิตศาสตร์ ม.4 เรื่องเซต ความหมายของเซต เซตจำกัด และเซตอนันต์ เซตว่าง และเอกภพสัมพัทธ์ ยูเนียน อินเตอร์เซกชันและคอมพลีเมนต์ของเซต สับเซตและเพาเวอร์เซต แผนภาพเวนน์-ออยเลอร์       ความหมายของเซต บทที่ 1 เซต (SET) http://web.ku.ac.th/schoolnet/snet2/knowledge_math/set/set5.htm เซต เป็นวิชาคณิตศาสตร์ที่ว่าด้วยเรื่องของกลุ่มของสิ่งต่างๆ ที่เราสนใจ กล่าวคือ ซึ่งนับว่าเป็นพื้นฐานคณิตศาสตร์เพื่อใช้เป็นพื้นฐานในการศึกษาคณิตศาสตร์ เรื่องอื่นๆ ในระดับต่อไปที่สาคัญ 1.1 ความหมายของเซต เซต เป็นคาที่ไม่ต้องนิยามความหมาย ( Undefine team ) แต่เราใช้คาว่า เซต แทนกลุ่มของสิ่งของ จานวน หรือสิ่งมีชีวิตที่การกล่วงถึง เช่น กลุ่ม กอง หมู่ เหลา โขลง คณะ พวก ชุด ฯลฯ เมื่อกล่าวถึงเซต สิ่งที่คำนึงถึงคือ เซตนั้นมีสิ่งใดบ้างที่สอดคล้องกันคากล่าวของเซต สิ่งที่อยู่ภายในเซตเรียกว่า “สมาชิกเซต” ( Element ) เช่น 1. เซตของจานวนคู่บวกที่น้อยกว่า 10 สมาชิกของเซตคือ 2, 4, 6 และ 8 2. เซตของสระในภาษาอังกฤษ สมาชิกเซต คือ a, e, i, o, และ u ในการศึกษาเรื่องเซต จะใช้สัญลักษณ์ € แทนคาว่า “เป็นสมาชิกของ” และนิยมตั้งชื่อให้กับคาบอกเซต ซึ่งชื่อเซตที่ตั้งนิยมใช้ตัวอักษรภาษาอังกฤษตัวพิมพ์ใหญ่เป็นชื่อของเซต เช่น A, B, C, เป็นต้น ตัวอย่าง เมื่อกล่าวคือ เซตของจานวนคู่บวกที่น้อยกว่า 10 กาหนดให้ชื่อเซตเป็น เซต A จะพิจารณาได้ว่า 2  €  A ( อ่านว่า 2 เป็นสมาชิกของเซต A ) 10 €  A ( อ่านว่า 10 ไม่เป็นสมาชิกของเซต A ) ตัวอย่าง 1 1. เซตของจำนวนนับที่มากกว่า 5 แต่น้อยกว่า 10 2. เซตของจังหวัดที่ขึ้นต้นด้วยพยัญชนะ “ข” 3. เซตของพยัญชนะของคาว่า “วิทยาลัย”                                    วิธีทำ 1. เซตของจำนวนเต็มที่มากกว่า 5 แต่น้อยกว่า 10 สมาชิกของเซตคือ 6, 7, 8, และ 9 2. เซตของจังหวัดที่ขึ้นต้นด้วยพยัญชนะ “ข” สมาชิกเซตคือ ขอนแก่น 3. เซตของพยัญชนะของคาว่า “วิทยาลัย” สมาชิกของเซตคือ ท, ย, ล และ ว ข้อสังเกต R แทนเซตของจำนวนจริง R+ แทนเซตของจำนวนจริงบวก R- แทนเซตของจำนวนจริงลบ Q แทนเซตของจำนวนตรรกยะ Q+ แทนเซตของจำนวนตรรกยะบวก Q- แทนเซตของจำนวนตรรกยะลบ I แทนเซตของจำนวนเต็ม I+ แทนเซตของจำนวนเต็มบวก I- แทนเซตของจำนวนเต็มลบ I0 แทนเซตของจำนวนเต็มศูนย์ N แทนเซตของจำนวนธรรมชาติหรือจานวนนับ      1. เซตจำกัด (Finite Set) เซตจำกัด (Finite Set) คือ เซตที่สามารถนับจำนวนสมาชิกได้ทั้งหมดและมีจำนวนที่แน่นอน เช่น A = {1, 2, 3, … ,20} จะเห็นได้ว่าเซต A สามารถบอกจำนวนสมาชิกได้ว่าเซตนี้มีจำนวนสมาชิกทั้งหมด 20 ตัว ดังนั้น เซต A จึงเป็นเซตจำกัด ลองดูอีกตัวอย่างกันนะครับ B = { 3 } จะเห็นได้ว่าเซต B สามารถที่จะบอกจำนวนสมาชิกได้ คือ 1 ตัว ดังนั้นเซต B จึงเป็นเซตจำกัด **หมายเหตุ เซตว่าง (Empty Set) ถือเป็นเซตจำกัด เขียนสัญลักษณ์แทนเซตว่างได้ดังนี้ หรือ { } 2. เซตอนันต์ (Infinite Set) เซตอนันต์ (Infinite Set) คือ เซตที่ไม่สามารถบอกจำนวนสมาชิกได้เพราะสมาชิกมีจำนวนมาก เช่น A = {1, 2, 3, … } จะเห็นได้ว่าเซต A ไม่สามารถบอกจำนวนสมาชิกตัวสุดท้ายที่อยู่ในเซตนี้ได้หมด ดังนั้นเซต A จึงเป็นเซตอนันต์ ลองมาดูกันอีกตัวอย่างนึง B = {3, 5, 7, …} จะเห็นได้ว่าเซต B ไม่สามารถบอกจำนวนสมาชิกที่เป็นจำนวนคี่ได้หมด ดังนั้นเซต B จึงเป็นเซตอนันต์  เซตว่าง (Empty Set) เซตว่าง คือ เซตที่ไม่มีสมาชิก หรือมีจำนวนสมาชิกในเซตเป็นศูนย์ สามารถเขียนแทนได้ด้วยสัญลักษณ์ {} หรือ Ø ตัวอย่างเช่น A = {x | x เป็นจำนวนเต็ม และ 1 < x < 2} ∴ A = Ø B = { x | x เป็นจำนวนเต็มบวก และ x + 1 = 0 } ∴ B = Ø เนื่องจากเราสามารถบอกจำนวนสมาชิกของเซตว่างได้ ดังนั้น เซตว่างเป็นเซตจำกัด เอกภพสัมพัทธ์ (Relative Universe) เอกภพสัมพัทธ์ คือ เซตที่กำหนดขอบเขตของสิ่งที่ต้องการศึกษา ซึ่งถือว่าเป็นเซตที่ใหญ่ที่สุด โดยมีข้อตกลงว่า ต่อไปจะกล่าวถึงสมาชิกของเซตนี้เท่านั้น จะไม่มีการกล่าวถึงสิ่งใดที่นอกเหนือไปจากสมาชิกของเซตที่กำหนดขึ้นนี้ โดยทั่วไปนิยมใช้สัญลักษณ์ U แทนเอกภพสัมพัทธ์ เช่น กำหนดให้ U = {1,2,3,4,5,6,7,8} A = {1,3,5,7} B = {2,4,8} หรือกำหนดให้ U = {x ε I+ | 1<x<20} A = {x ε U | x=n+3 เมื่อ n เป็นจำนสวนเต็มคี่บวก} B = {x ε U | x=n+3 เมื่อ n เป็นจำนสวนเต็มคู่บวก} นั่นคือทั้ง A และ B เป็นสับเซตของ Uยูเนียน อินเตอร์เซกชัน และคอมพลีเมนต์ของเซต เป็นส่วนหนึ่งของการกระทำระหว่างเซต เรานิยมเขียนออกมาในสองรูปแบบด้วยกันคือแบบสมการ และแผนภาพเวนน์-ออยเลอร์ เราลองมาดูกันครับว่ายูเนียน อินเตอร์เซกชัน และคอมพลีเมนต์ของเซต เป็นอย่างไรพร้อมตัวอย่าง ยูเนียน (Union) ยูเนียน (Union) มีนิยามว่า เซต A ยูเนียนกับเซต B คือเซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A หรือ เซต B หรือทั้ง A และ B สามารถเขียนแทนได้ด้วย สัญลักษณ์ A ∪ B ตัวอย่างเช่น 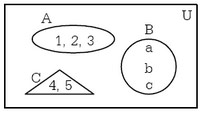A ={1,2,3} B= {3,4,5} ∴ A ∪ B = {1,2,3,4,5} เราสามารถเขียนการยูเนี่ยนลงในแผนภาพได้ดังนี้ อินเตอร์เซกชัน (Intersection) อินเตอร์เซกชัน (Intersection) มีนิยามคือ เซต A อินเตอร์เซกชันเซต B คือ เซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A และเซต B สามารถเขียนแทนได้ด้วยสัญลักษณ์ A ∩ B ตัวอย่างเช่น A ={1,2,3} B = {3,4,5} ∴ A ∩ B = {3} เราสามารถเขียนการอินเตอร์เซกชันลงในแผนภาพได้ดังนี้ คอมพลีเมนต์ (Complements) คอมพลีเมนต์ (Complements) มีนิยามคือ ถ้าเซต A ใดๆ ในเอกภพสัมพัทธ์ U แล้วคอมพลีเมนต์ของเซต A คือ เซตที่ประกอบด้วยสมาชิกที่เป็นสมาชิกของ U แต่ไม่เป็นสมาชิกของ A สามารถเขียนแทนได้ด้วยสัญลักษณ์ A’ ตัวอย่างเช่น U = {1,2,3,4,5} A ={1,2,3} ∴ A’ = {4,5}  เราสามารถเขียนการคอมพลีเมนต์ของเซตลงในแผนภาพได้ดังนี้ สับเซต (Subset) ถ้าสมาชิกทุกตัวของ A เป็นสมาชิกของ B แล้ว จะเรียกว่า A เป็นสับเซตของ B จะเขียนว่า เซต A เป็นสับเซตของเซต B แทนด้วย A ⊂ B ถ้าสมาชิกบางตัวของ A ไม่เป็นสมาชิกของ B จะเรียกว่า A ไม่เป็นสับเซตของ B เซต A ไม่เป็นสับเซตของเซต B แทนด้วย A ⊄ B สมบัติของสับเซต 1) A ⊂ A (เซตทุกเซตเป็นสับเซตของตัวมันเอง) 2) A ⊂ U (เซตทุกเซตเป็นสับเซตของเอกภพสัมพัทธ์) 3) ø ⊂ A (เซตว่างเป็นสับเซตของทุกๆ เซต) 4) ถ้า A ⊂ ø แล้ว A = ø 5) ถ้า A ⊂ B และ B ⊂ C แล้ว A ⊂ C (สมบัติการถ่ายทอด) 6) A = B ก็ต่อเมื่อ A ⊂ B และ B ⊂ A 7) ถ้า A มีจำนวนสมาชิก n ตัว สับเซตของเซตจะมีทั้งสิ้น 2n สับเซต สับเซตแท้ นิยาม A เป็นสับเซตแท้ของ B ก็ต่อเมื่อ A⊂B และ A ≠ B ตัวอย่าง กำหนดให้ A = { a , b , c } จงหาสับเซตแท้ทั้งหมดของ A วิธีทำ สับเซตแท้ของ A ได้แก่ ø, {a} , {b} ,{c} , {a,b} , {a ,c} , {b,c} มีจำนวนสมาชิกทั้งสิ้น 7 สับเซต หมายเหตุ ถ้า A มีจำนวนสมาชิก n ตัว สับเซตแท้ของเซตA จะมีทั้งสิ้น 2n –1 สับเซต 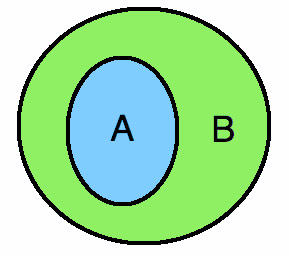เราสามารถเขียนความสัมพันธ์ของสับเซตออกมาในรูปของแผนภูมิได้ดังนี้ครับจากรูปแสดงได้ว่า A⊂B เพาเวอร์เซต (Power Set) คำว่า เพาเวอร์เซต เป็นคำศัพท์เฉพาะ ซึ่งใช้เป็นชื่อเรียกเซตเซตหนึ่งที่เกี่ยวข้องกับเรื่องสับเซต เพาเวอร์เซตของ A เขียนแทนด้วย P(A) P(A) คือเซตที่มีสับเซตทั้งหมดของ A เป็นสมาชิก สมบัติของเพาเวอร์เซต ให้ A , B เป็นเซตใดๆ 1) ø ⊂ P(A) 2) A ⊂ P(A) 3) P(A) ≠ ø 4) P(A) ⊂ P(B) ก็ต่อเมื่อ A ⊂ B 5) ถ้า A มีสมาชิก n ตัว P(A) จะมีสมาชิก 2n ตัว แผนภาพเวนน์-ออยเลอร์ แผนภาพเวนน์-ออยเลอร์ คือแผนภาพที่ใช้เขียนแทนเซตโดยใช้รูปปิดอะไรก็ได้ เช่น รูปสามเหลี่ยม รูปวงกลม รูปวงรี แต่จะนิยมเขียนแทนเอกภพสัมพัทธ์ด้วยรูปสี่เหลี่ยมผืนผ้า แล้วเขียนแทนเซตในเอกภพสัมพัทธ์ด้วยรูปวงกลม ตัวอย่างการเขียนแผนภาพเวนน์-ออยเลอร์ กำหนด U={0,1,2,3,...,10},A={2,4,6}$\mathcal{U}=\{0,1,2,3,...,10\},A=\{2,4,6\}$ และ B={1,3,5}$B=\{1,3,5\}$ เขียนเป็นแผนภาพเวนน์-ออยเลอร์ได้ดังนี้ เซต A$A$ และ B$B$ ไม่มีสมาชิกที่เหมือนกันเลย แสดงว่าทั้ง 2$2$ วง แยกออกจากกันชัดเจน เราใส่ตัวเลขที่เป็นสมาชิกของ A$A$ และ B$B$ ลงในวงกลมทั้ง 2$2$ เซต ตัวเลขที่เหลือในเอกภพสัมพัทธ์ที่ไม่ได้อยู่ทั้งในเซต A$A$ และ B$B$ เราต้องเขียนแสดงไว้ในกรอบสี่เหลี่ยมผืนผ้านอกวงกลม ตัวอย่างการเขียนแผนภาพเวนน์-ออยเลอร์ กำหนด U={0,1,2,3,...,10},A={1,2,3,4,5}$\mathcal{U}=\{0,1,2,3,...,10\},A=\{1,2,3,4,5\}$ และ B={3,5,6,7,8}$B=\{3,5,6,7,8\}$ เขียนเป็นแผนภาพเวนน์-ออยเลอร์ได้ดังนี้ ในกรณีนี้ เซต A$A$ และ B$B$ มีสมาชิกที่เหมือนกันคือ 3$3$ และ 5$5$ ดังนี้น ทั้งสองเซตจึงมีบางส่วนซ้อนกัน 3$3$ และ 5$5$ จึงอยู่ในส่วนที่เซต A$A$ และ B$B$ ซ้อนกัน  ตัวอย่างการเขียนแผนภาพเวนน์-ออยเลอร์ กำหนด U={0,1,2,3,...,10},A={1,2,3}$\mathcal{U}=\{0,1,2,3,...,10\},A=\{1,2,3\}$ และ B={1,2,3,4,5,6}$B=\{1,2,3,4,5,6\}$ เขียนเป็นแผนภาพเวนน์-ออยเลอร์ได้ดังนี้ ในกรณีนี้จะเห็นว่า A⊂B$A\subset B$ ดังนั้น เซต A$A$ ทั้งวงจึงเข้าไปอยู่ในเซต B$B$ แผนภาพเวนน์-ออยเลอร์ กับการดำเนินการของเซต แผนภาพเวนน์-ออยเลอร์ ช่วยให้เรามองความสัมพันธ์ระหว่างเซต และการดำเนินการของเซตได้ชัดเจนขึ้น 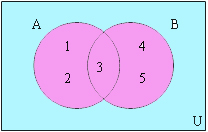1.  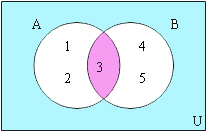ยูเนี่ยน ส่วนที่แรเงาแสดงพื้นที่ของ A∪B$A\cup B$ 2.  อินเตอร์เซกชั่น ส่วนที่แรเงาแสดงพื้นที่ของ A∩B$A\cap B$ 3.  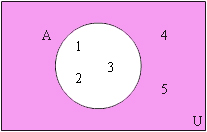ผลต่าง ส่วนที่แรเงาแสดงพื้นที่ของ A−B$A-B$ 4.  คอมพลีเมนต์ ส่วนที่แรเงาแสดงพื้นที่ของ Ac